パターン１ - かずのたしなみ（統計環境Rによる） @Wiki

パターン１（１変数、１グループの場合）

データ例（ウェイトレスの時給）

８００円　１０００円　１１００円　９５０円　１２００円　９００円　１０５０円　８００円

Ｒにデータ入力

x <- c(800,1000,1100,950,1200,900,1050,800)

パターン１で使える統計処理の方法

グラフ表示

> barplot(x) #棒グラフをかく

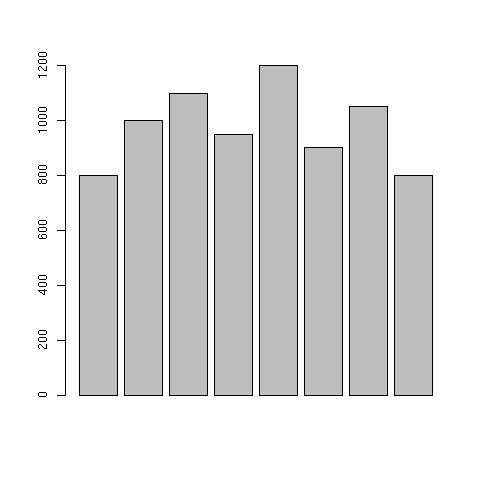
画面にグラフを出すなら上記の命令１行だけで済む。
今回はｊｐｅｇファイルを貼付けているが、
ｊｐｅｇファイルにグラフを書き出すのは以下の通り。

> jpeg("myplot.jpg") #jpegファイルで出力
> barplot(x) #棒グラフをかく
> dev.off()         #出力を標準に戻す

基礎等計量

> summary(x)
  Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   800     875     975     975    1062    1200 

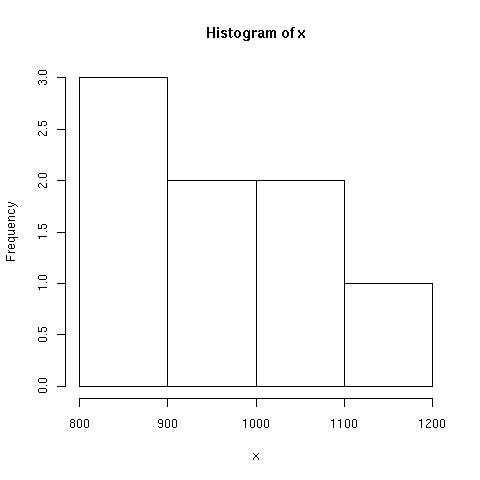
度数分布表とヒストグラム

> hist(x)

母平均の区間推定

母平均の検定

つまり今手にしたデータは、母集団から無作為抽出したものと考えるのである。
母平均の区間推定と母平均の検定の二つは、１つの命令で一気に解決する。

>t.test(x,mu=975)

       One Sample t-test

data:  x 
t = 0, df = 7, p-value = 1
alternative hypothesis: true mean is not equal to 975 
95 percent confidence interval:
  856.7688 1093.2312 
sample estimates:
mean of x 
     975 

95 percent confidence interval:
とは、母集団の平均値（母平均）がこの区間（856.7688〜1093.2312）のどこかにある確率が95％の確率ということ。逆に言うと、この区間から母平均がはみ出す確率は５％以下だということ。

サンプルの平均値975と、母集団の平均値が等しくないという対立仮説は、ｐ値＝１＞０．０５で棄却できない。
サンプルが少なすぎるのである。

石村貞夫(1994)『すぐわかる統計処理』（東京図書）トップページに戻る